本文經授權轉載自研之成理

【前言】

書讀百遍，其義自見！最近又重讀了下N?rskov的這篇綜述（Nature Chem. 2009, 1, 37-46），簡單地將論文中的一些核心觀點梳理下分享給大家，希望對大家有所幫助。論文標題： Towards the computational design of solid catalysts, DOI:?10.1038/nchem.121.

?

?

【背景介紹】

A. 基本原則：催化劑的催化性能本質上都是由其電子結構決定的，因此催化劑的設計從根本上來說是要綜合考慮組成，物理結構等因素來調控材料的電子結構。

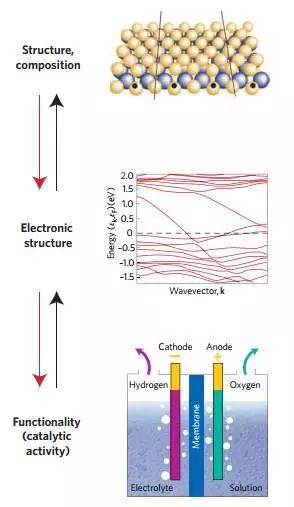
Figure 1

B. 目前理論計算的主要出發點：為什么這個催化劑能夠表現出優異的性能？（驗證型）

C.實際需求：給定催化反應條件，如何知道需要哪種材料？（探究型）

?

簡單地來說，理論計算最基本的一個發展路線就是如何從驗證發展到探究，如何從證明發展到預測。只有當理論計算真正實現預測的時候，才能算是理論計算的成熟期。

?

【催化活性的趨勢（trends）和描述因子（descriptors）】

理論計算簡化實際催化體系的基本方法：將催化劑簡化為一個個相互獨立的晶面，所有的表面都會對催化反應有所貢獻，而貢獻最大的就是主要的活性中心。

?

對于一個催化反應而言，找到一個衡量催化劑活性的descriptor以及明確不同催化劑的活性趨勢是非常重要的，這是理解催化劑結構性能關系以及利用理論計算預測催化劑的基礎。

?

?

為什么在理論計算中總是會看到一些火山圖？

注意，火山圖一般出現在多步反應途徑中。這其實跟過渡態的穩定性有關系，某一過渡態比較穩定的話，形成這個過渡態就比較容易（勢壘較低），但相應地從這個過渡態變到另一個狀態就會困難一些（勢壘會更高）；而相反，若過渡態的穩定性較差的話，形成中間體會很困難（勢壘較高），而變到另一個狀態會比較容易（勢壘會比較低）。所以，多步驟反應中會經常存在這樣的平衡（Sabatier principle）。

?

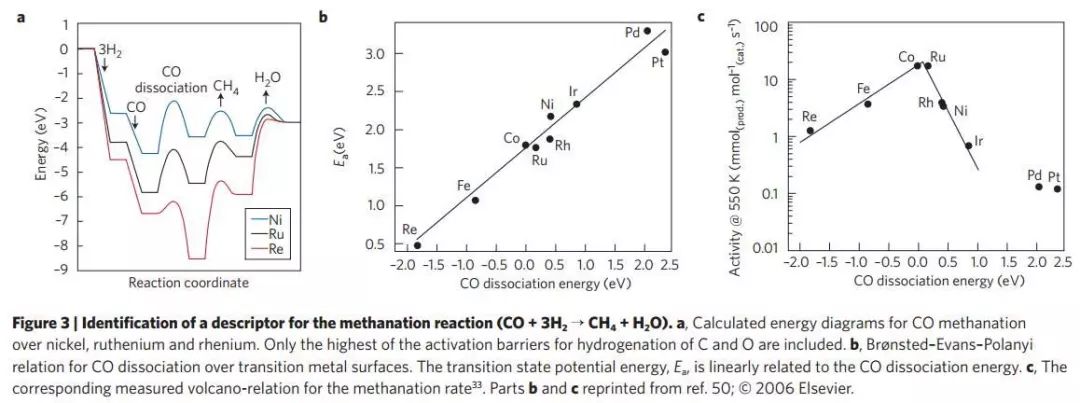
這里作者舉了個例子：CO+3H2–CH4+H2O, 其中CO的解離以及CH4+H2O的生成就存在這樣的一個平衡，如果CO解離成C+O在催化劑表面很穩定，那么形成CH4+H2O的勢壘就會比較高，而相反則解離比較困難，這種平衡的存在不可避免的就會出現一個火山型曲線，如Figure 3C所示。

?

其實得到火山型曲線是比較簡單的，問題是采用怎樣的descriptor來將這個催化過程的規律體現出來。這里之所以采用CO的解離能是因為根據BEP原則，CO解離成C+O的活化能跟CO解離能之間是線性相關的（Figure 3b），所以可以用CO的解離能作為descriptor，說明的規律就是剛才說的那個平衡。

?

備注：BEP原則（Bell–Evans–Polanyi principle）的表達式Ea=Eo+αΔH。其中ΔH是反應的焓變，Ea是反應活化能，Eo和α是特征參數。

?

類似的其實在電化學析氧（OER）反應中，通常采用的descriptor是ΔG(O)*-ΔG(HO)*，請查閱：ChemCatChem 2011, 3, 1159 – 1165.

?

【催化劑電子結構的描述因子】

比較經典的是d-band模型，而這個也正是Norskov所提出來的：the higher in energy the?d-states are relative to the highest occupied state- the Fermi energy- of the metal, the stronger the interaction with adsorbate states.

具體的例子大家看下圖就知道了

在OER催化中，Yang Shao-Horn課題組(Science, 2011,334,1383)曾提出：The filling of the surface transition metal antibonding states of eg-orbital parentage is a more appropriate descriptor for catalysis.

?

【催化劑的設計】

其實原理上很簡單，在得到了一個火山型曲線之后（Figure 3C），火山型曲線峰值所對應的肯定是最好的，但是很多情況下這些材料都比較貴，比如CO+3H2—CH4+H2O這個反應而言，最好的催化劑Ru和Co都挺貴的，那么如何設計一個便宜一點的催化劑呢？一個基本的原則就是從火山曲線的兩邊選擇材料來進行復合（合金化），比如說Ni和Fe，一個在左支，一個在右支，通過復合可以讓其性能變得更好，具體如下圖所示。

【催化選擇性】

?催化選擇性一般用不同反應路徑的勢壘差來進行衡量，勢壘差越大選擇性越高。以乙烯的環氧化為例，它的中間態可以是環氧乙烷也可以是乙醛，生成環氧乙烷的話就會直接脫附，而生成乙醛則會進一步深度氧化。The?difference in energy between these two transition states thus becomes?a good descriptor for the selectivity of an EO catalyst, and catalysts,?which favour the transition state going towards EO, can be sought?computationally. 從Figure 7可以看出，加入一定量的Cu可以提高Energy difference，因此可以提高選擇性（當然這里也要考慮一個問題，就是到底誰更容易生成的問題，所要優化的應該是更容易生成EO的催化劑）。

?

備注:文章講到了好幾個例子，剛興趣的朋友自己去查看原文哈

?

【難點與展望】

1. 對于催化劑的設計而言，除了高活性，選擇性，低成本這些可以用于計算的性能指標外，催化劑穩定性，抗中毒性等等也是非常重要的參數，而這些在理論計算中并不能全面覆蓋到。

2. DFT計算的結果應該跟催化反應條件緊密結合起來，以合成氨為例，氨氣濃度不一樣，理想的催化劑就會不一樣，低氨氣濃度下Fe最優，高氨氣濃度下Ru最優。

?

3. 如何將催化劑的載體有效地納入到計算的范疇中？

?總的來說，理論計算仍處在發展階段，不過目前結合原位表征手段，DFT計算來研究催化反應機理已經成為了主流，如何進一步完善理論計算，最終實現理論指導實踐是個漫漫求索的過程！

?

在整個研究探索過程中，理論與實驗的全方位合作對理解催化反應機理、高效催化劑的選擇、催化劑設計等方面至關重要。